Abstract
The Fractal Mosaic algorithm is a rotation, scale, and translation invariant photomosaic algorithm. While traditional photomosaics create a larger image out of smaller square images on a rectangular grid, Fractal Mosaics creates a larger image out of rectangular images that can be placed at arbitrary locations, can be scaled to any size, and can be rotated by any angle.
This is accomplished with a combination of image search (i.e. image retrieval) algorithms and an image registration algorithm developed with NASA funding by Siavash Zokai and George Wolberg at the City College of New York (pdf).

Figure 1: Fractal Mosaic created with graffiti image set (best viewed large)
For more Fractal Mosaics, check out my Flickr page.
Figure 2 shows three traditional photomosaics created with AndreaMosaic using the same image set and target image.

Figure 2: Traditional Photomosaics using large tiles (left), medium sized tiles (middle), and small tiles (right)
As can be seen, using large tiles (left), finer details are lost. Using small tiles (right), we capture target image details, but can’t see individual image detail. Using medium size tiles (middle), we get a compromise between the two. Fractal Mosaics aims to create mosaics that capture both target image details and individual image details, in an aesthetically interesting way.
Many people have, of course, created photomosaic variants with similar aims. Too many to list here. Some of my favorite photomosaic pioneers that I’m aware of: Tsevis, Village9991, and StellaMe. If I’m unaware of your work, contact me!
By allowing for arbitrary placement, rotation, and scaling of the “library images” (images making up the mosaic), there are an many more possible matches to evaluate. This allows for larger, often more aesthetically interesting matches than possible with traditional photomosaics. However, searching such a large solution space on a personal computer presents a challenging problem. This “paper” presents my solution to this problem (two years worth of unpaid work...). It explains the algorithm in depth for those wishing to hack the Matlab code. It should also aid those using the code to create mosaics, as understanding how the algorithm works will help tweak parameters that shape mosaic output.
The following sections will walk you through the main pieces of the Fractal Mosaic algorithm.
- Introduction/Problem Statement
- Image Registration
- Image Search (Retrieval)
- Mosaic Rendering
- Conclusions / Future Directions
Introduction / Problem Statement
In a traditional photomosaic, the number of possible matches is large but still easily manageable on a modern PC. The number of possible matches is simply the number of “tiles” (square areas in the target image) times the number of library images. For each tile, a similarity metric is calculated (root mean squared (rms) error, typically) for every library image. The library image with the smallest rms error is placed in the mosaic.
In a Fractal Mosaic, the number of possible possible matches is effectively infinite. For example, let’s say we use 5,000 library images, a 3072 x 1024 pixel target image, and do the following fairly rough quantization of the possible translations, rotations, and scalings:
- 2 degree rotations (180 possible rotations)
- Every fifth pixel is a possible placement location (629,145 possible translations)
- 50 possible scaling values
This gives us (180 rotations) x (629,145 translations) x (50 scalings) x (5,000 library images) = 28,311,525,000,000 possible matches to search. Or ~28 trillion matches. Obviously, a brute force search is not feasible (I tried).
Fractal Mosaics tackles this complexity with three main strategies. One strategy is inherent in the “Log-polar” image registration algorithm at the core of Fractal Mosaics. This algorithm uses a coarse-to-fine multi-resolution framework, whereby estimates computed in lower resolution images are used as initial guesses in higher resolution images. An in-depth explanation of how log polar registration is implemented in Fractal Mosaics is given in the Log-polar Registration section.
The second main strategy is to use an image search algorithm to filter out library images that are statistically unlikely to produce a match. Details on this can be found in the Image Search (Retrieval) section.
The third main strategy for reducing the number of matches evaluated is to look for large matches first, then not look for smaller matches “under” those matches (i.e., don’t look for matches in areas where we’ve already placed an image). This saves considerable computation. However, it will cause the algorithm to miss aesthetically better matches under the placed matches. For this reason, Fractal Mosaics can be configured to also look for alternate matches under placed images. All matches can optionally be output to PNG files that can be loaded into Photoshop for later compositing.
Image Registration
Image registration is generally defined as the lining up of images misaligned due to rotation, scale, and position (translation). The field of image registration is mature, constituting of several decades of research. The key insight of Fractal Mosaics is that image registration algorithms can be employed to efficiently search the photomosaic solution space. Instead of evaluating every possible rotation, scaling, and translation for every library image (computationally impossible), we can use image registration to efficiently estimate these parameters. Once these parameters are estimated, they are used to rotate, scale, and translate the library image in question to best match the target image. A similarity metric (rms error in this case) is applied. If the rotated, scaled, and translated library image scores high enough on the similarity metric, it is placed in the mosaic.
Registration Algorithm Choice
After an initial survey of the image registration literature, a frequency domain image registration algorithm was evaluated; specifically, Fourier-Mellin-based image registration, as implemented in this Matlab code. This would have been much more computationally efficient than the spatial domain algorithm eventually chosen, as rotation, scale, and translation are efficiently recovered in one step. However, this technique proved not robust enough for the photomosaic application. This is likely because it relies more heavily on the assumption made by all image registration algorithms: that the two images being matched are of the same object/scene. In photomosaics however, we are matching parts of the target image to random library images. The assumption that the library images are rotated, scaled, and translated versions of the target image is weak.
An image registration algorithm that operates in the spatial domain was tried; specifically, the “Log-polar registration” algorithm found in the paper “Robust Image Registration Using Log-Polar Transform” (pdf). This algorithm proved very robust. And most importantly, it met the main aesthetic criteria: for any two images presented to the algorithm, it aligned them the way a human would. To test this claim out for yourself, check out the video below showing the algorithm at work matching library images to a target image.
The downside to Log-polar registration is increased computation. Because Log-polar registration only recovers rotation and scale, to recover translation, it must be applied to every location (pixel) in the target image. The location resulting in the lowest rms error is then chosen as the estimate. This creates a lot of extra computation. To mitigate this, the authors of the algorithm use a coarse-to-fine multi-resolution framework, whereby estimates computed in lower resolution images are used as initial guesses in higher resolution images. The following section reviews Log-polar registration in Fractal Mosaics.
Log Polar Image Registration
In “Robust Image Registration Using Log-Polar Transform”, the authors lay out a “two module” approach. First, a “Log-polar registration” module estimates rotation, scale, and translation. Then, a second module uses a nonlinear least squares optimization method to refine this estimation and obtain sub-pixel accuracy. Since Fractal Mosacis does not require sub-pixel accuracy, and the log polar registration module was found to be accurate enough for this application, just the log-polar registration module is implemented.
The following sections overview how Log-polar registration works in general. For nitty gritty details on how the multi-resolution framework was adapted to the photomosaic problem, see the Image Registration Algorithm Steps page.
Polar Coordinates
To understand Log-polar registration, we briefly review polar coordinates.
When transforming from Cartesian to polar coordinates, each pixel location (x,y) is represented as a radius and angle (r,a), where r is the distance from the center of the image (xC,yC), and a is the angle in degrees from the x-axis.
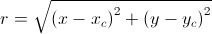
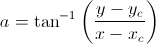
Figure 3 illustrates the polar transform using an image of Abraham Lincoln. Here we see a crop of the Lincoln image (a), the Lincoln image rotated by 90° (c), and the log-polar transforms of both ((b) and (d)).
Figure 3: Polar transform of Lincoln image rotated 90°
As can be seen, in the polar space, the 90 degree rotation manifests as a circular shift along the x-axis of the polar image (i.e. the angle axis). If we take the cross-correlation of the polar transformed images ((b) and (d)), the maximum of the cross-correlation gives us the rotation. However, scale cannot be recovered from the cross-correlation.
Log-polar Transform
Here’s where we take advantage of some math magic. According to the product rule of logarithms,
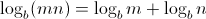
Assuming we scale an image up by a factor of 3, in the polar space, this is equivalent to multiplying the radius values by 3.
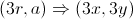
If we apply the log function to the radius values (i.e. the Log-polar transform),
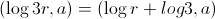
Scale now manifests as a scalar phase shift, log(3), in the radius axis (i.e. x-axis). Rotation still manifests as a phase shift in the angle axis (i.e. y-axis), as it did in the straight polar transform. We can now recover both scale and rotation from the cross-correlation of the log-polar transformed images. Magic!
Figure 4 shows a crop of the Lincoln image (a), the Lincoln image rotated by 45° and scaled up by a factor of 2 (c), and the log-polar transforms of both ((b) and (d)).

Figure 4: Log-polar transform of Lincoln image rotated 45° and scaled by 2X
As can be seen, the 45° rotation shows up as a circular shift along the x-axis (i.e. angle axis) and the 2X scaling shows up as a phase shift along the y-axis (i.e. angle axis).
Rotation and Scale Estimation
To estimate rotation and scale, we take the cross-correlation of the log-polar transformed images ((b) and (d) in Figure 4). The maximum of the cross-correlation (dark red peak) corresponds to rotation and scale (equations for calculating rotation and scale from peak can be found in the code).
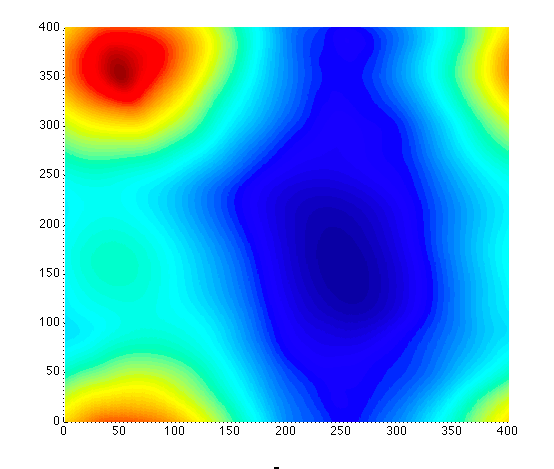
Figure 5: Cross-correlation of the log-polar transformed images ((b) and (d) in Figure 4)
For computational efficiency, the cross-correlation is computed in the Fourier domain using 2D FFTs,
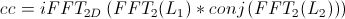
where L1 and L2 are the log-polar transformed library and target images, respectively.
Recovering Translation
As mentioned previously, Log-polar registration does not recover translation. It assumes the two images presented to it line up, except for rotation and scale differences. To recover translation, the algorithm must be applied to every location (pixel). The translation resulting in the best match (i.e. lowest rms error) is then chosen as the translation estimate.
To reduce computation, the authors of Log-polar registration implement a multi-resolution framework, whereby estimates computed in lower resolution images are used as initial guesses in higher resolution images. At each resolution, rotation and scale estimates are computed for every location. The location(s) that result in an rms error below a threshold are sent to the next higher resolution for refining.
The video below shows the algorithm at work evaluating library images. As can be seen, most library images aren't evaluated beyond the lowest resolution (8x8). This is because most library images, even when rotated and scaled to best match the target image, aren't good enough matches to evaluate at higher resolutions. For details on error thresholds and other implementation details, see the Image Registration Algorithm Steps page.
Image Search (Retrieval) Filtering
An image search (i.e. retrieval) algorithm is used to filter out statistically unlikely matches before the computationally intensive image registration step (i.e., don’t waste cycles trying to match a white part of the target image with an image of the night sky). Specifically, Fractal Mosaics performs Content-Based Image Retrieval (CBIR), similar to Google’s search by image feature. The “search image” (the part of the target image we’re looking to match), is compared to every library image using a similarity metric. Then only the most similar library images are evaluated using image registration.
Numerous similarity metrics were evaluated, including histograms, standard deviation, Hu moments, General Fourier Descriptors (GFD), and Fourier Mellin (FM) shape descriptors. The metrics which performed best were histograms, GFDs, and standard deviation. These metrics were combined to create a custom similarity metric that slightly outperformed any individual similarity metric. This metric is currently only used in black and white mode, as I ran out of time to extend it to color. For color, a relatively simple yet effective similarity metric (histogram distance in the HSV color space) is used. Implementation details for black and white and color retrieval are given in the sections below.
Black and White
For black and white mosaics, a custom similarity metric was developed. This metric combines three commonly used similarity metrics: histogram distance, General Fourier Descriptor (GFD) distance, and difference in standard deviation. For a given pixel location, the histogram, GFD, and standard deviation of the “search image”, or target tile (piece of the target image we’re matching) are calculated. These are then compared to the histogram, GFD, and standard deviation of every library image, which have been precomputed. For the histogram and GFD, euclidean distance is computed. For standard deviation, the absolute difference is used.
The histogram distance, GFD distance, and standard deviation difference are then input into respective Probability Density Functions (PDFs), which were calculated empirically using 430,500 pseudo-random samples of the solution space. The sum of the output of these PDFs is the “Match PDF”.
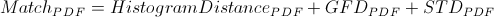
All library images are then sorted by their Match PDF scores, and only the images with the highest probability of being a match are sent to the image registration step.
Color
When creating a color mosaic, the similarity metric is the distance between 3D histograms in the HSV color space. The code used to implement this (and implementation details) can be found here. Thanks to Theodoros Giannakopoulos for sharing!
Mosaic Rendering
The main Fractal Mosaic script renders a version of the mosaic as it goes. Alternately, after running the main script, a separate rendering script can be run, which gives the user the ability to play with different rendering parameters. Notably, you can set:
- Whether the images will be placed on top of the target image or on a black background.
- How much blending to do between images. Blending is currently done with a simple linear gradient. The user sets a variable which sets the percentage of the image that will be blended. Figure 6 shows a blending window that uses the default, 25%.
- Whether to use color images or not. For color mosaics, this is typically a no brainer. However, you can render a black and white mosaic using the color versions of the black and white images used for matching. This can often lead to interesting, accidental results, as illustrated in Figure 7.
Figure 6: Default blending window (25% of image edge blended)

Figure 7: Example of using color images when rendering a black and white mosaic
Conclusion / Next Steps
Considerable effort has been put into automating the entire mosaic creation process, and making beautiful mosaics. However, Fractal Mosaics is not programmed to make artistic or conceptual choices on individual images. Therefore, its most promising use in some use cases will be generating input into a another process (e.g. a human using Photoshop or other software).
Considerable effort has been put into optimizing the code, both on the algorithmic and code level. However, it still takes a considerable amount of time to run (e.g. 6-8 hrs for a black and white mosaic with medium complexity, 2-3 days for a equivalent color mosaic). Promising optimization strategies include translation from Matlab to another language such as C/C++, accelerating key functions on the GPU (graphics card), and cloud computing (e.g. run on Amazon's EC2, etc.).
Considerable effort has been put into creating art with the code. However, Fractal Mosaics constitutes a new tool. One that exposes many new possibilities. These possibilities, as with any "new medium", will take time to flesh out. It is my hope that by putting this code out there, artists will take up the challenge and create art I can't even imagine. Have at it!

